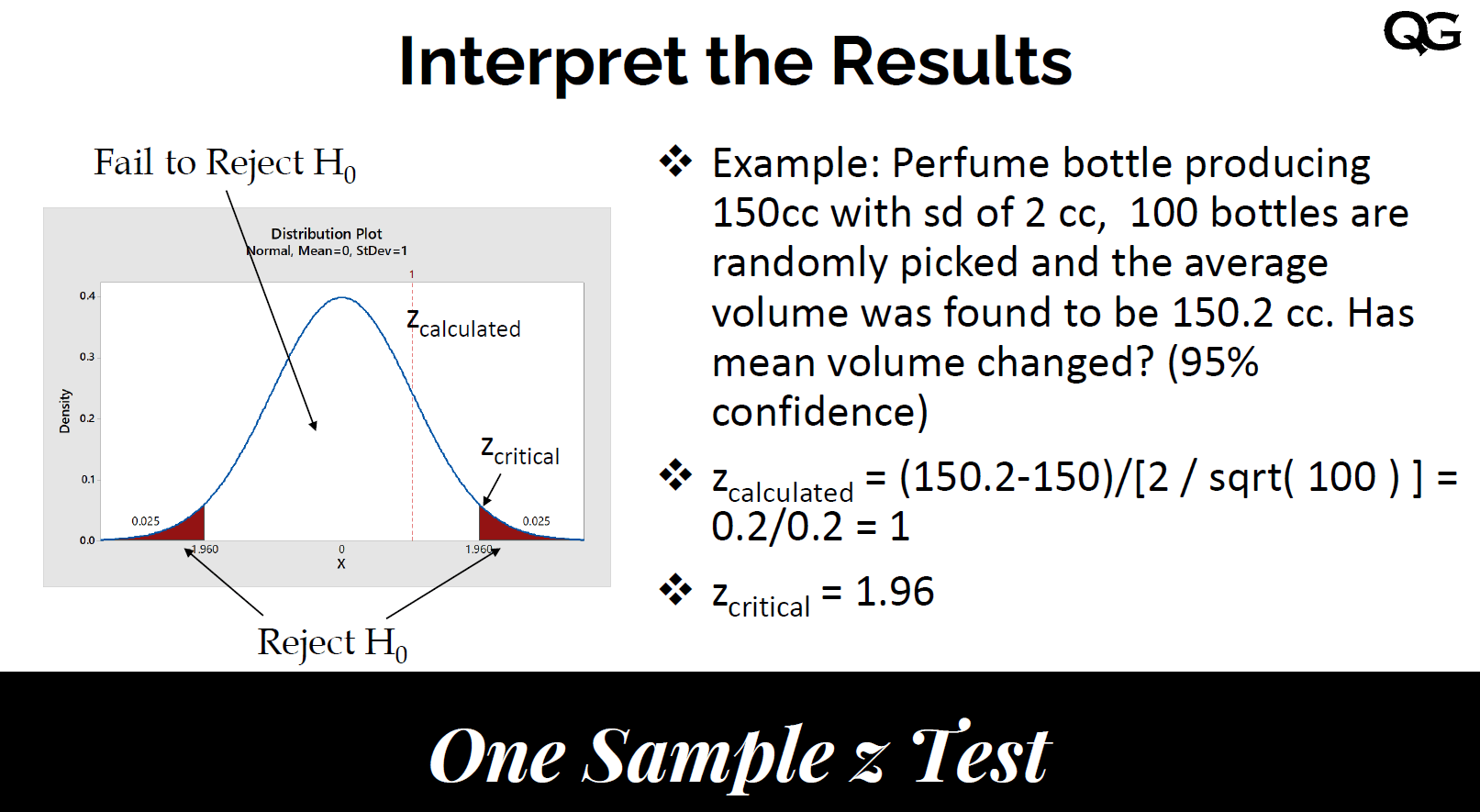
One-Sample Z Test

 One-Sample Z Test

The **one-sample Z test**, **t-test**, and **F test** are statistical methods used to analyze data and test hypotheses in various research situations. Each test has specific applications based on sample size, data distribution, and the nature of the hypothesis being tested. Below is a detailed comparison of these tests, including when to use each.

## One-Sample Z Test

### Definition

The one-sample Z test is used to determine whether the mean of a single sample differs significantly from a known population mean when the population variance is known. It is applicable primarily when the sample size is large (typically $$n \geq 30$$).

### When to Use

- **Large Sample Size**: When the sample size is 30 or more.

- **Known Population Variance**: When the population standard deviation is known.

- **Normal Distribution**: When the data is approximately normally distributed.

### Example

A researcher wants to test if the average height of a sample of students differs from the known average height of students in the population, which is 170 cm. If the sample size is 50 and the population standard deviation is known, a Z test would be appropriate.

## T-Test

### Definition

The t-test is used to compare the means of one or two groups when the population variance is unknown and the sample size is small (typically $$n < 30$$). There are different types of t-tests, including one-sample, independent samples, and paired samples t-tests.

### When to Use

- **Small Sample Size**: When the sample size is less than 30.

- **Unknown Population Variance**: When the population standard deviation is not known.

- **Normal Distribution**: When the data is normally distributed.

### Example

If a researcher wants to determine whether the average test score of a class of 25 students is significantly different from the national average score of 75, they would use a one-sample t-test.

## F Test

### Definition

The F test is used to compare the variances of two or more groups. It is often employed in the context of ANOVA (Analysis of Variance) to determine if there are any statistically significant differences between the means of multiple groups.

### When to Use

- **Comparing Variances**: When the goal is to assess whether the variances of two or more groups are significantly different.

- **Multiple Groups**: When comparing means across multiple groups (more than two).

### Example

A researcher may use an F test to compare the variances of test scores among three different teaching methods to see if one method has more variability than the others.

## Summary of Differences

| Test Type        | Sample Size Requirement | Known Variance | Purpose                                   | Example Application                                     |

|------------------|-------------------------|----------------|-------------------------------------------|--------------------------------------------------------|

| One-Sample Z Test| $$n \geq 30$$           | Known          | Compare sample mean to a known population mean | Testing if average height of students differs from a known average |

| T-Test           | $$n < 30$$              | Unknown        | Compare sample mean to a known population mean or compare means of two groups | Testing if average test scores of a small class differ from national average |

| F Test           | Any size                | Not applicable | Compare variances of two or more groups   | Comparing variances of test scores among different teaching methods |

## Conclusion

Understanding the differences between the one-sample Z test, t-test, and F test is crucial for selecting the appropriate statistical method based on the research design, sample size, and data characteristics. Each test serves a specific purpose, helping researchers draw valid conclusions from their data.

Citations:

[1] https://brandalyzer.blog/2010/12/05/difference-between-z-test-f-test-and-t-test/

[2] https://www.cuemath.com/data/z-test/

[3] https://testbook.com/key-differences/difference-between-t-test-and-f-test

[4] https://www.shiksha.com/online-courses/articles/difference-between-z-test-and-t-test-blogId-158833

[5] https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6813708/

[6] https://www.investopedia.com/terms/z/z-test.asp

[7] https://www.simplilearn.com/tutorials/statistics-tutorial/z-test-vs-t-test

[8] https://www.scribbr.com/statistics/chi-square-tests/